Phanxuan Phuc

fakerphan

I’m a AI Engineer in Vin Bigdata. And I summarize research papers in these topics:

6 mins read

Published by: ByteDance AI Lab & Nanjing University & UC Santa Barbara

REDER

REDER stands for “Reversible Duplex Transformer” which is a Transformer model where its both ends can simultaneously input and output a distinct language thus enabling reversible machine translation by simply flipping the input and output ends. REDER was proposed by ByteDance AI lab in 2022 and published in their paper: Duplex Sequence-to-Sequence Learning for Reversible Machine Translation. The official code for this paper can be found in the following GitHub repository: REDER.

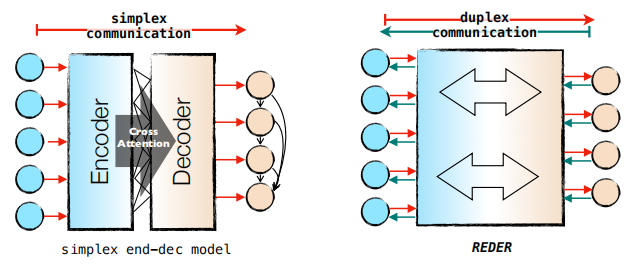
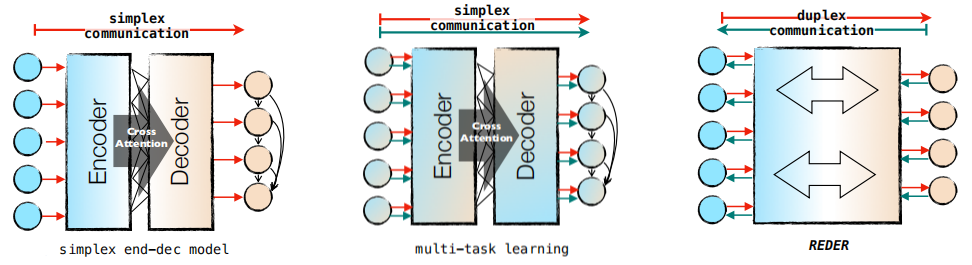
In this paper, they proposed an alternative approach for utilizing bidirectional supervisions called duplex sequence-to-sequence learning which is better than the typical sequence-to-sequence learning where the encoder learns to represent the source language and the decoder learns to generate the target language, and multi-task learning where the encoder learns to represent multiple language simultaneously while the decoder learns to generate multiple language simultaneously.

Note:
The name “Duplex” comes from telecommunications and computer networking where the “simplex” communication means the communication channel is unidirectional while the “duplex” communication is bidirectional.

We should note that building duplex seq2seq networks is non-trivial; and that’s because of the following reasons:

  • Reversibility:
    Typical encoder-decoder networks such as Transformers are irreversible, i.e., one cannot just obtain its inverse function by flipping the same encoder-decoder network.

  • Homogeneity:
    The decoder works autoregressively, while the encoder works in a non-autoregressive manner.

That’s why REDER is designed without explicit encoder and decoder division introducing two solutions (Reversible Duplex Transformer layers and the Symmetric Network architecture) to address the reversibility and homogeneity issues respectively as we are going to see next.

Reversible Duplex Transformer Layer

The following figure shows the overall architecture of REDER where we can see that it has two ends: the source end (left) and the target end (right). As illustrated, REDER is composed of a series of identical Reversible Duplex Transformer layers. Since the network has two ends, it defines a forward mapping function $f_{\theta}^{\rightarrow}:X \rightarrow Y$ and a reverse mapping function $f_{\theta}^{\leftarrow}:Y \rightarrow X$ that satisfy the following reversibility: $f_{\theta}^{\rightarrow} = \left( f_{\theta}^{\leftarrow} \right)^{- 1}$ and $f_{\theta}^{\leftarrow} = \left( f_{\theta}^{\rightarrow} \right)^{- 1}$.

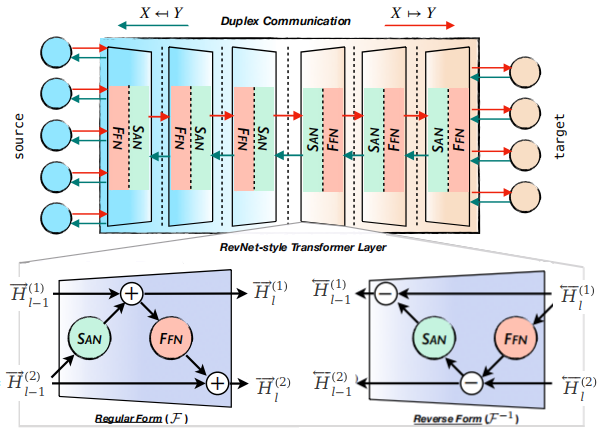
The Reversible Duplex Transformer layer is adopted from the Reversible Networks (RevNet) where each layer is composed of two sub-layers: a multi-head self-attention (SAN) and a feed-forward network (FFN) with a special reversible design to ensure a duplex behavior.

Given a sentence pair $\left( x,y \right)$, the inner representations of each layer in divided into two directions:

  • The forward direction $\overrightarrow{H}_l$ which is the concatenation of two halves $\left\lbrack \overrightarrow{H}_l^{\left( 1 \right)},\ \overrightarrow{H}_l^{\left( 2 \right)} \right\rbrack$:
\[{\overrightarrow{H}}_{l} = F_{l}\left( \left\lbrack {\overrightarrow{H}}_{l - 1}^{\left( 1 \right)},\ {\overrightarrow{H}}_{l - 1}^{\left( 2 \right)} \right\rbrack \right) = \left\lbrack {\overrightarrow{H}}_{l}^{\left( 1 \right)},\ {\overrightarrow{H}}_{l}^{\left( 2 \right)} \right\rbrack\] \[{\overrightarrow{H}}_{l}^{\left( 1 \right)} = {\overrightarrow{H}}_{l - 1}^{\left( 1 \right)} + \text{SAN}\left( {\overrightarrow{H}}_{l - 1}^{\left( 2 \right)} \right)\] \[{\overrightarrow{H}}_{l}^{\left( 2 \right)} = {\overrightarrow{H}}_{l - 1}^{\left( 2 \right)} + \text{FFN}\left( {\overrightarrow{H}}_{l}^{\left( 1 \right)} \right)\]
  • The backward direction $\overleftarrow{H}_l$ which is the concatenation of two halves $\left\lbrack \overleftarrow{H}_l^{\left( 1 \right)},\ \overrightarrow{H}_l^{\left( 2 \right)} \right\rbrack$:
\[{\overleftarrow{H}}_{l - 1} = F_{l}^{- 1}\left( \left\lbrack {\overleftarrow{H}}_{l}^{\left( 1 \right)},\ {\overleftarrow{H}}_{l}^{\left( 2 \right)} \right\rbrack \right) = \left\lbrack {\overleftarrow{H}}_{l - 1}^{\left( 1 \right)},\ {\overleftarrow{H}}_{l - 1}^{\left( 2 \right)} \right\rbrack\] \[{\overleftarrow{H}}_{l - 1}^{\left( 2 \right)} = {\overleftarrow{H}}_{l}^{\left( 2 \right)} + FFN\left( {\overleftarrow{H}}_{l}^{\left( 1 \right)} \right)\] \[{\overleftarrow{H}}_{l - 1}^{\left( 1 \right)} = {\overleftarrow{H}}_{l}^{\left( 1 \right)} + \text{SAN}\left( {\overleftarrow{H}}_{l - 1}^{\left( 2 \right)} \right)\]

Note:
The attention mechanism used in this paper is a relative self-attention proposed in the “Self-attention with relative position representations” paper, instead of the original one proposed in the Transformer paper.

Symmetric Network

As discussed earlier, using reversible duplex transformer layers solves the reversibility problem. Now, let’s see how to solve the Homogeneity problem. To achieve homogeneous computations, the model must satisfy the following cycle consistency:

\[\forall x \in X:f_{\theta}^{\leftarrow}\left( f_{\theta}^{\rightarrow}\left( x \right) \right) = x,\ \ \ \ \ \ \ \ \forall y \in Y:f_{\theta}^{\rightarrow}\left( f_{\theta}^{\leftarrow}\left( y \right) \right) = y\]

One solution is to make the network symmetric which can be done as follows: given an network of $L$ layers, the layers starting from $1$ till $\frac{L}{2}$ will be in reverse form, whereas the layers starting from $\frac{L}{2} + 1$ to $L$ be in regular form:

\[f_{\theta}^{\rightarrow}\left( x \right) \triangleq F_{1}^{- 1} \circ \text{...} \circ F_{\frac{L}{2}}^{- 1} \circ F_{\frac{L}{2} + 1} \circ \text{...} \circ F_{L}\left( x \right)\] \[f_{\theta}^{\leftarrow}\left( y \right) \triangleq F_{L} \circ \text{...} \circ F_{\frac{L}{2} + 1} \circ F_{\frac{L}{2}}^{- 1} \circ \text{...} \circ F_{1}^{- 1}\left( y \right)\]

And this property means that the REDER model works in a fully non-autoregressive fashion in both reading and generating sequences. Specifically, given an input sequence $x = \left( x_{1},\ …x_{n} \right)$, the i-th element of REDER’s input $x_{i}$ is the concatenation of two copies of the embedding of $x_{i}$ as shown below:

\[{\overrightarrow{H}}_{0,i} = \left\lbrack {\overrightarrow{H}}_{0,i}^{\left( 1 \right)},\ {\overrightarrow{H}}_{0,i}^{\left( 2 \right)} \right\rbrack = \left\lbrack e\left( x_{i} \right),\ e\left( x_{i} \right) \right\rbrack\]

Once the forward computation is done, the concatenation of the output of the model $\left\lbrack {\overrightarrow{H}}_{L,i}^{\left( 1 \right)},\ {\overrightarrow{H}}_{L,i}^{\left( 2 \right)} \right\rbrack$ serves as the representations of target translation after a softmax operation is performed to measure the similarity between itself and the concatenated embedding of ground-truth reference $\left\lbrack e\left( y_{i} \right),\ e\left( y_{i} \right) \right\rbrack$ to obtain the prediction probability:

\[p\left( y_{i} \middle| x;\ \theta \right) = \text{softmax}\left( \frac{1}{2}{\left\lbrack e\left( y_{i} \right),\ e\left( y_{i} \right) \right\rbrack\ }^{T}.\left\lbrack {\overrightarrow{H}}_{L,i}^{\left( 1 \right)},\ {\overrightarrow{H}}_{L,i}^{\left( 2 \right)} \right\rbrack \right)\]

Objective Function

Given a parallel dataset $\mathcal{D}_{x,y} = \left( x^{\left( n \right)},\ y^{\left( n \right)} \right)_{n = 1}^{N}$ ,the final objective of REDER is to minimize the following objective function:

\[\mathcal{L}\left( \theta;\mathcal{D}_{x,y} \right) = \sum_{n = 1}^{N}\left( - \log\left( p_{\text{ctc}}\left( y^{\left( n \right)} \middle| x^{\left( n \right)};\theta \right) \right) - log\left( p_{\text{ctc}}\left( x^{\left( n \right)} \middle| y^{\left( n \right)};\theta \right) \right) + \lambda_{\text{fba}}\mathcal{L}_{\text{fba}}\left( x^{\left( n \right)} \middle| y^{\left( n \right)};\theta \right) + \lambda_{\text{fba}}\mathcal{L}_{\text{fba}}\left( y^{\left( n \right)} \middle| x^{\left( n \right)};\theta \right) + \lambda_{\text{cc}}\mathcal{L}_{\text{cc}}\left( x^{\left( n \right)};\theta \right) + \lambda_{\text{cc}}\mathcal{L}_{\text{cc}}\left( y^{\left( n \right)};\theta \right) \right)\]

Where:

  • $p_{\text{ctc}}\left( y^{\left( n \right)} \middle| x^{\left( n \right)};\theta \right)$ is the CTC loss of the forward direction, while $p_{\text{ctc}}\left( x^{\left( n \right)} \middle| y^{\left( n \right)};\theta \right)$ is the CTC loss of the backward direction.

  • $\mathcal{L}_{\text{fba}}\left( x^{\left( n \right)} \middle| y^{\left( n \right)};\theta \right)$ is the forward-backward agreement of the forward direction, while $\mathcal{L}_{\text{fba}}\left( y^{\left( n \right)} \middle| x^{\left( n \right)};\theta \right)$ is the forward-backward agreement of the backward direction. This loss function is calculated via the following formula knowing that $sg()$ is the stop-gradient operation:

\[\mathcal{L}_{\text{fba}}\left( x \middl| y;\theta \right) = \frac{1}{L}\sum_{l = 1}^{L}{1 - \cos\left( {\overrightarrow{H}}_{l},\ \text{sg}\left( {\overleftarrow{H}}_{l} \right) \right)}\]
  • $\mathcal{L}_{\text{cc}}\left( x^{\left( n \right)};\theta \right)$ is the cycle consistency loss of the forward direction, while $\mathcal{L}_{\text{cc}}\left( y^{\left( n \right)};\theta \right)$ is the cycle consistency of the backward direction. This loss function is calculated via the following formula:
\[\mathcal{L}_{\text{cc}}\left( x;\theta \right) = distance\left( x,\ f_{\theta}^{\leftarrow}\left( f_{\theta}^{\rightarrow}\left( x \right) \right) \right)\]
  • $\lambda_{\text{fba}}$ and $\lambda_{\text{cc}}$ are the coefficients of the auxiliary losses.

Note:
Training REDER is done in a a two-stage training setting, where we first train REDER without using any auxiliary losses until a predefined number of updates, and then activate the additional losses and continue training the model until convergence.

Experiments

In the paper, they evaluated REDER on two standard translation benchmarks: WMT14 English↔German (4.5M training pairs), and WMT16 English↔Romanian (610K training pairs). REDER was implemented using fairseq framework and it consists of $12$ stacked layers. The number of head is $8$, the model dimension is $512$, and the FFN is $2048$. For regularization, they used a dropout rate of $0.1$ and L2-regularization of $0.01$ and label smoothing with $\epsilon = 0.1$. Also, they both $\lambda_{\text{fba}}$ and $\lambda_{\text{cc}}$ to $0.1$ for all experiments. All models were trained for 300K updates with a batch size of approximately 64K tokens. For scoring, they average the best 5 checkpoints to obtain the final model.

The following table shows the a comparison between REDER and other existing models knowing that all NAT models were trained with Knowledge Distillation (KD), also “MTL” stands for “multitask learning” and “BT” stands for “back-translation”. (row 4 ∼ row 9) employ greedy decoding while (row 10 ∼ row 14) employ beam search decoding with beam size of 20.

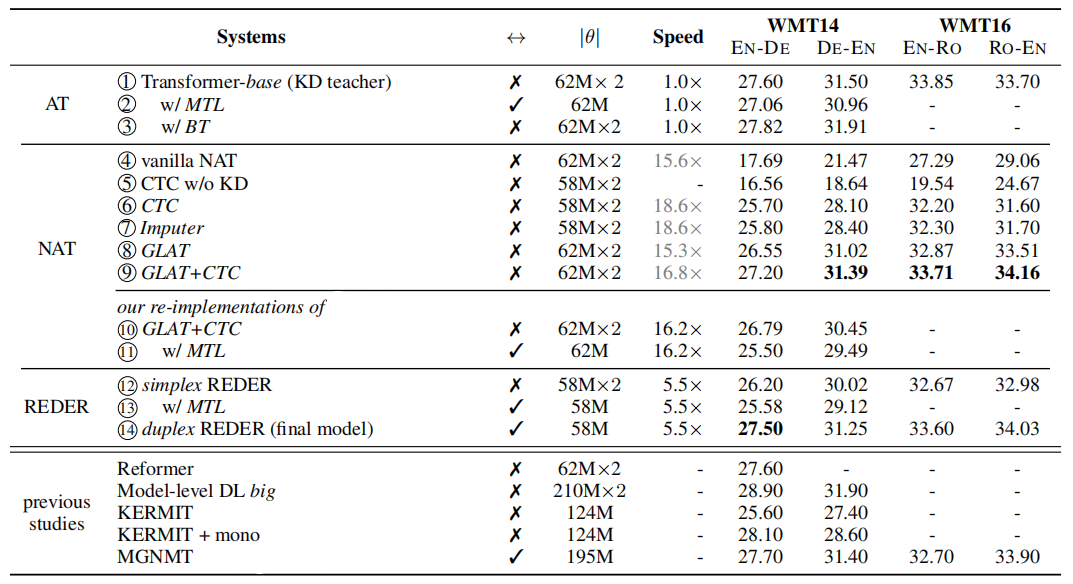
From the previous table we can see:

  • REDER achieves competitive results compared with strong NAT baselines.

  • Duplex learning has more potential than multitask learning and back-translation.

  • REDER performs on par with autoregressive Transformer

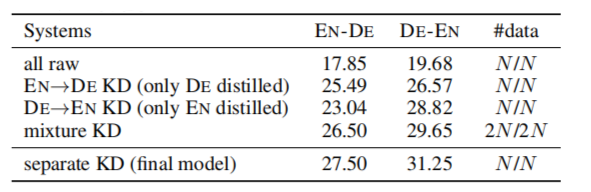
Like other NAT approaches, they found out that REDER heavily relies on knowledge distillation. The following table shows that the accuracy of REDER without KD significantly drops:

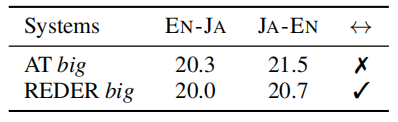
To examine whether REDER can generalize to distant languages, they conducted experiments on WMT20 English↔Japanese dataset. The following table shows that REDER can achieve very close results compared with Auto-regressive Transformer (AT) in such a large-scale scenario with distant languages: